APIO 2009 - Digging for Oil

Explanation

Official Explanation: APIO 2009 solutions document

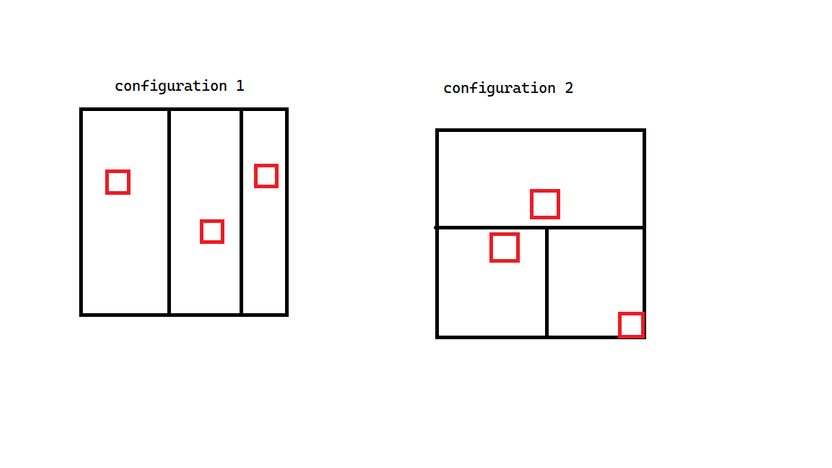
We want the three largest disjoint $K\times K$ squares with the largest total sums. Note that every pair of rectangles must be on opposite sides of some line. This leaves us with two basic configurations; either there are two parallel lines dividing the squares or there are two perpendicular lines. The configurations are illustrated below:

Note that solutions need to account for all possible rotations of these configurations.

Configuration 1

In this configuration, we can find the answer for each non-middle subrectangle using the method in Configuration 2. However, we need to use another recurrence to find the middle rectangle. WLOG let the subrectangles be arranged in top-down order, as the left-right order can be found similarly. Let $d{p}_{i,j}$ be the answer for the rows in interval $[i,j]$. Obviously $d{p}_{i,i+l}$ has no answers if $l<k-1$. We can also manually find $d{p}_{i,i+k}$ manually as a base case. Next, note that $d{p}_{i,j}$ consists of all $K\times K$ squares counted in $d{p}_{i+1,j}$ and $d{p}_{i,j-1}$. Then, there are just the squares counted in row $i$ and row $j$, which is just $d{p}_{i,i+k-1}$ and $d{p}_{j-k+1,j}$ respectively. Thus, the recurrence is $d{p}_{i,j}=\max (\max (d{p}_{i+1,j},d{p}_{i,i+k-1}),\max (d{p}_{i,j-1},d{p}_{j-k+1,j})).$ Note that intervals must be traversed from smallest to largest.

Configuration 2

It suffices to use prefix sums. From each corner, find the sum of the values of all points that can be reached solely by travelling towards that corner from a point $(i,j)$, and store the value with $(i,j)$. We can use this to find the total amount of oil for the $K\times K$ squares on each corner of $(i,j)$. These values help us find the maximum amount of oil in a $K\times K$ square on each corner of $(i,j)$. We then perform some casework for each reflection to get the answer.

Code

1#include <bits/stdc++.h>
2
3using namespace std;
4
5#define MAXN 1505
6
7int m,n,k,dp[MAXN][MAXN][2],pp[MAXN][MAXN][4],pq[MAXN][MAXN],ar[MAXN][MAXN];
8int main()
9{
10    ios_base::sync_with_stdio(0);